Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex Class Reference

Description

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>
class Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex

Vertex node.

These list nodes contain all information about a vertex and are the objects returned (by reference) when a vertex node iterator (VertexIterator or ConstVertexIterator) is dereferenced.

Definition at line 1188 of file Graph.h.

#include <Graph.h>

Public Member Functions
const size_t &	id () const
	Unique vertex ID number. More...
size_t	nInEdges () const
	Number of incoming edges. More...
size_t	nOutEdges () const
	Number of outgoing edges. More...
size_t	degree () const
	Number of incident edges. More...
boost::iterator_range< EdgeIterator >	inEdges ()
	List of incoming edges. More...
boost::iterator_range< ConstEdgeIterator >	inEdges () const
	List of incoming edges. More...
boost::iterator_range< EdgeIterator >	outEdges ()
	List of outgoing edges. More...
boost::iterator_range< ConstEdgeIterator >	outEdges () const
	List of outgoing edges. More...
VertexValue &	value ()
	User-defined value. More...
const VertexValue &	value () const
	User-defined value. More...

Member Function Documentation

id()

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

const size_t& Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::id ( ) const

inline

Unique vertex ID number.

Vertices within a graph are numbered consecutively starting at zero, and this method returns the vertex's ID number. ID numbers are unrelated to the order in which vertices are inserted, although in the absense of vertex erasure they will be assigned consecutively. Vertex ID numbers are stable over insertion of vertices and edges and the erasure of edges, but are not stable over vertex erasure. In order to obtain constant-time vertex erasure (at least when it has no incident edges), after a vertex is erased the largest-ID vertex is renumbered to fill the gap.

Time complexity is constant.

Definition at line 1208 of file Graph.h.

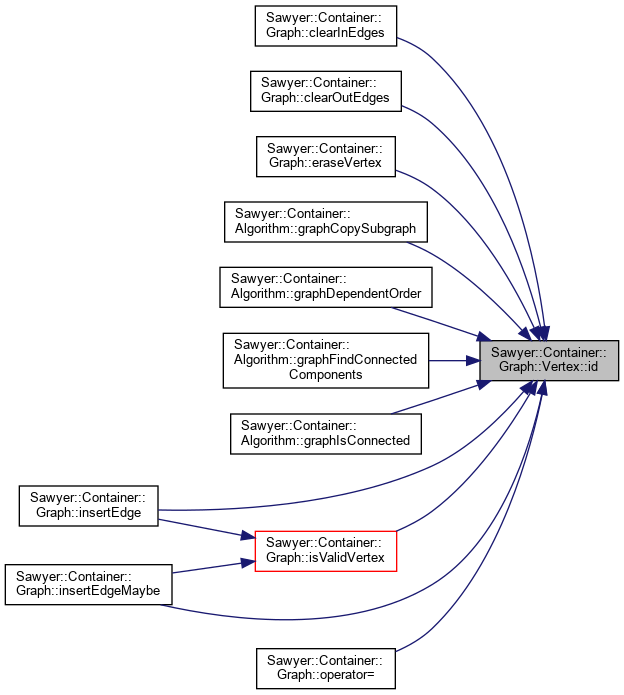
Referenced by Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::clearInEdges(), Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::clearOutEdges(), Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::eraseVertex(), Sawyer::Container::Algorithm::graphCopySubgraph(), Sawyer::Container::Algorithm::graphDependentOrder(), Sawyer::Container::Algorithm::graphFindConnectedComponents(), Sawyer::Container::Algorithm::graphIsConnected(), Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::insertEdge(), Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::insertEdgeMaybe(), Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::isValidVertex(), and Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::operator=().

Here is the caller graph for this function:

inEdges() [1/2]

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

boost::iterator_range<EdgeIterator> Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::inEdges ( )

inline

List of incoming edges.

Returns a sublist of edges whose target vertex is this vertex. The return value is a pair of iterators which delineate the edges. The traversal is in no particular order. Edge iterators are equality-comparable with one another even when the come from different sublists. See EdgeIterator for details.

Time complexity is constant.

Definition at line 1219 of file Graph.h.

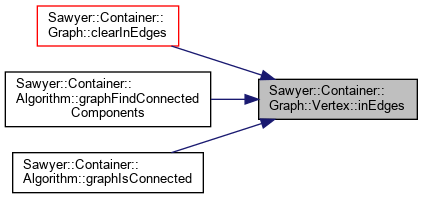
Referenced by Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::clearInEdges(), Sawyer::Container::Algorithm::graphFindConnectedComponents(), and Sawyer::Container::Algorithm::graphIsConnected().

Here is the caller graph for this function:

inEdges() [2/2]

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

boost::iterator_range<ConstEdgeIterator> Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::inEdges ( ) const

inline

List of incoming edges.

Returns a sublist of edges whose target vertex is this vertex. The return value is a pair of iterators which delineate the edges. The traversal is in no particular order. Edge iterators are equality-comparable with one another even when the come from different sublists. See EdgeIterator for details.

Time complexity is constant.

Definition at line 1224 of file Graph.h.

outEdges() [1/2]

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

boost::iterator_range<EdgeIterator> Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::outEdges ( )

inline

List of outgoing edges.

Returns a sublist of edges whose source vertex is this vertex. The return value is a pair of iterators which delineate the edges. The traversal is in no particular order. Edge iterators are equality-comparable with one another even when the come from different sublists. See EdgeIterator for details.

Time complexity is constant.

Definition at line 1240 of file Graph.h.

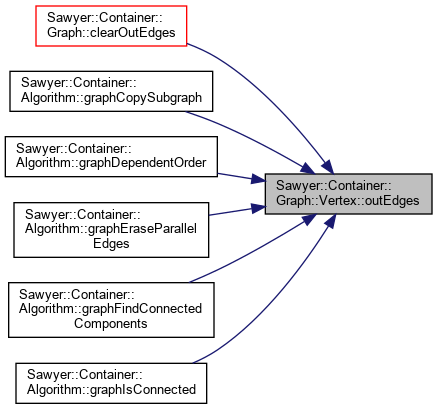
Referenced by Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::clearOutEdges(), Sawyer::Container::Algorithm::graphCopySubgraph(), Sawyer::Container::Algorithm::graphDependentOrder(), Sawyer::Container::Algorithm::graphEraseParallelEdges(), Sawyer::Container::Algorithm::graphFindConnectedComponents(), and Sawyer::Container::Algorithm::graphIsConnected().

Here is the caller graph for this function:

outEdges() [2/2]

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

boost::iterator_range<ConstEdgeIterator> Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::outEdges ( ) const

inline

List of outgoing edges.

Returns a sublist of edges whose source vertex is this vertex. The return value is a pair of iterators which delineate the edges. The traversal is in no particular order. Edge iterators are equality-comparable with one another even when the come from different sublists. See EdgeIterator for details.

Time complexity is constant.

Definition at line 1245 of file Graph.h.

nInEdges()

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

size_t Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::nInEdges ( ) const

inline

Number of incoming edges.

Returns the in-degree of this vertex, the length of the list returned by inEdges.

Definition at line 1255 of file Graph.h.

nOutEdges()

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

size_t Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::nOutEdges ( ) const

inline

Number of outgoing edges.

Returns the out-degree of this vertex, the length of the list returned by outEdges.

Definition at line 1262 of file Graph.h.

Referenced by Sawyer::Container::Algorithm::graphEraseParallelEdges().

Here is the caller graph for this function:

degree()

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

size_t Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::degree ( ) const

inline

Number of incident edges.

Returns the total number of incident edges, the sum of nInEdges and nOutEdges. Self-edges are counted two times: once for the source end, and once for the target end.

Definition at line 1270 of file Graph.h.

value() [1/2]

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

VertexValue& Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::value ( )

inline

User-defined value.

Each vertex stores one user-defined value whose type is specified as the V parameter of the Graph template (a.k.a., the VertexValue type). This method returns a reference to that data, which was copied into the graph when this vertex was inserted. This is also the value that is returned when a vertex value iterator (VertexValueIterator or ConstVertexValueIterator) is dereferenced.

Time complexity is constant.

Definition at line 1284 of file Graph.h.

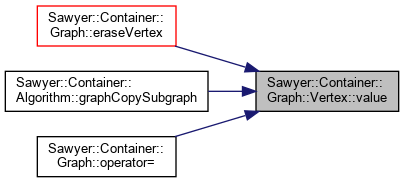
Referenced by Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::eraseVertex(), Sawyer::Container::Algorithm::graphCopySubgraph(), and Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::operator=().

Here is the caller graph for this function:

value() [2/2]

template<class V = Nothing, class E = Nothing, class VKey = GraphVertexNoKey<V>, class EKey = GraphEdgeNoKey<E>, class Alloc = DefaultAllocator>

const VertexValue& Sawyer::Container::Graph< V, E, VKey, EKey, Alloc >::Vertex::value ( ) const

inline

User-defined value.

Each vertex stores one user-defined value whose type is specified as the V parameter of the Graph template (a.k.a., the VertexValue type). This method returns a reference to that data, which was copied into the graph when this vertex was inserted. This is also the value that is returned when a vertex value iterator (VertexValueIterator or ConstVertexValueIterator) is dereferenced.

Time complexity is constant.

Definition at line 1285 of file Graph.h.

---

The documentation for this class was generated from the following file:

• Graph.h