Incomplete Tiles
8.3. Incomplete Tiles#
Optimal performance for tiled loops is achieved when the loop iteration count is a multiple of the tile size. When this condition does not exist, the implementation is free to execute the partial loops in a manner that optimizes performance, while preserving the specified order of iterations in the complete-tile loops.
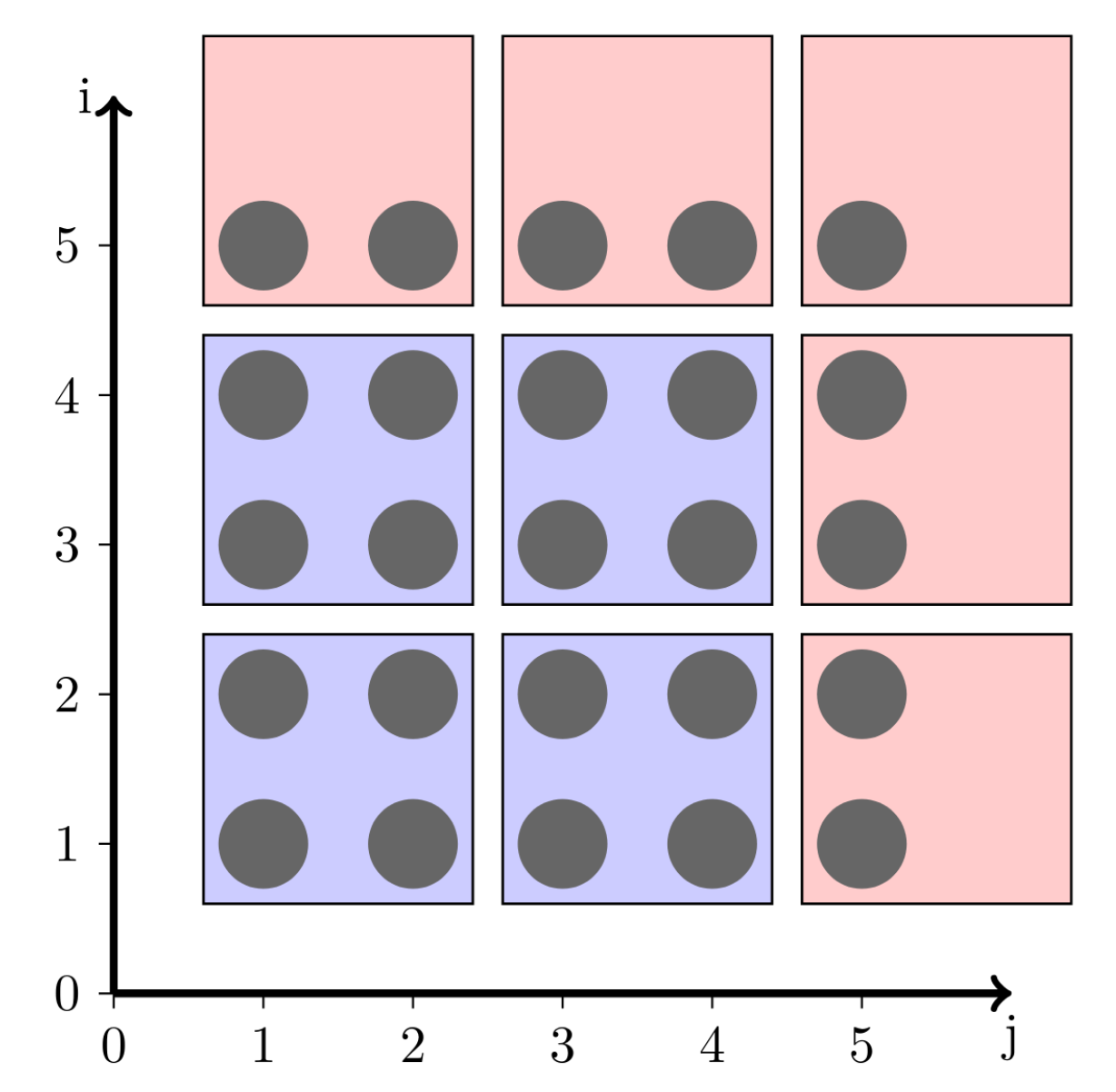
Figure 8.1a shows an example of a 2-by-2 tiling for a 5-by-5 iteration space. There are nine resulting tiles. Four are complete 2-by-2 tiles, and the remaining five tiles are partial tiles.
|
|
(A) 2-dimensional tiling with partial tiles |
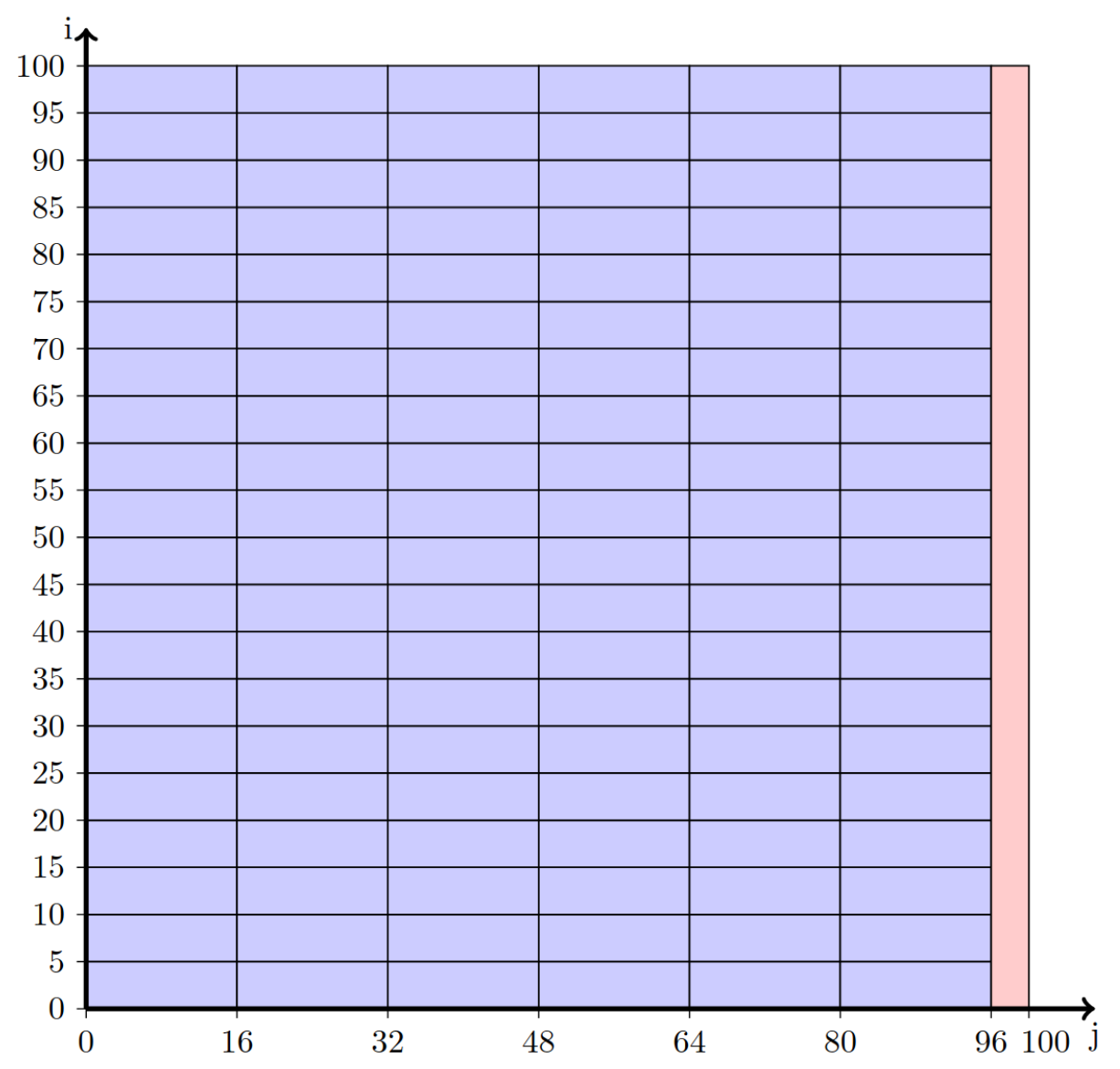
(B) Partial tiles of Example partial_tile.1 |
FIGURE 8.1: Tiling illustrations
In the following example, function func1 uses the tile construct with a sizes(4,16) tiling clause. Because the second tile dimension of 16 does not evenly divide into the iteration count of the j-loop, the iterations corresponding to the remainder for the j-loop correspond to partial tiles as shown in Figure 8.1b. Each remaining function illustrates a code implementation that a compiler may generate to implement the tile construct in func1 .
The order of tile execution relative to other tiles can be changed, but execution order of iterations within the same tile must be preserved. Implementations must ensure that dependencies that are valid with any tile size need to be preserved (including tile size of 1 and tiles as large as the iteration space).
Functions func2 through func6 are valid implementations of func1. In func2 the unrolling is illustrated as a pair of nested loops with a simple adjustment in the size of the final iteration block in the j2 iteration space for the partial tile.
Performance of the implementation depends on the hardware architecture, the instruction set and compiler optimization goals. Functions func3 , func4 , and func5 have the advantage that the innermost loop for the complete tile is a constant size and can be replaced with SIMD instructions. If the target platform has masked SIMD instructions with no overhead, then avoiding the construction of a remainder loop, as in func5 , might be the best option. Another option is to use a remainder loop without tiling, as shown in func6 , to reduce control-flow overhead.
//%compiler: clang
//%cflags: -fopenmp
/*
* name: partial_tile.1
* type: C
* version: omp_5.1
*/
int min(int a, int b){ return (a < b)? a : b; }
void func1(double A[100][100])
{
#pragma omp tile sizes(4,16)
for (int i = 0; i < 100; ++i)
for (int j = 0; j < 100; ++j)
A[i][j] = A[i][j] + 1;
}
void func2(double A[100][100])
{
for (int i1 = 0; i1 < 100; i1+=4)
for (int j1 = 0; j1 < 100; j1+=16)
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j2 = j1; j2 < min(j1+16,100); ++j2)
A[i2][j2] = A[i2][j2] + 1;
}
void func3(double A[100][100])
{
// complete tiles
for (int i1 = 0; i1 < 100; i1+=4)
for (int j1 = 0; j1 < 96; j1+=16)
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j2 = j1; j2 < j1+16; ++j2)
A[i2][j2] = A[i2][j2] + 1;
// partial tiles / remainder
for (int i1 = 0; i1 < 100; i1+=4)
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j = 96; j < 100; j+=1)
A[i2][j] = A[i2][j] + 1;
}
void func4(double A[100][100])
{
for (int i1 = 0; i1 < 100; i1+=4) {
// complete tiles
for (int j1 = 0; j1 < 96; j1+=16)
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j2 = j1; j2 < j1+16; ++j2)
A[i2][j2] = A[i2][j2] + 1;
// partial tiles
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j = 96; j < 100; j+=1)
A[i2][j] = A[i2][j] + 1;
}
}
void func5(double A[100][100])
{
for (int i1 = 0; i1 < 100; i1+=4)
for (int j1 = 0; j1 < 100; j1+=16)
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j2 = j1; j2 <j1+16; ++j2)
if (j2 < 100)
A[i2][j2] = A[i2][j2] + 1;
}
void func6(double A[100][100])
{
// complete tiles
for (int i1 = 0; i1 < 100; i1+=4)
for (int j1 = 0; j1 < 96; j1+=16)
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j2 = j1; j2 < j1+16; ++j2)
A[i2][j2] = A[i2][j2] + 1;
// partial tiles / remainder (not tiled)
for (int i = 0; i < 100; ++i)
for (int j = 96; j < 100; ++j)
A[i][j] = A[i][j] + 1;
}
!!%compiler: gfortran
!!%cflags: -fopenmp
! name: partial_tile.1
! type: F-free
! version: omp_5.1
subroutine func1(A)
implicit none
double precision :: A(100,100)
integer :: i,j
!$omp tile sizes(4,16)
do i = 1, 100
do j = 1, 100
A(j,i) = A(j,i) + 1
end do; end do
end subroutine
subroutine func2(A)
implicit none
double precision :: A(100,100)
integer :: i1,i2,j1,j2
do i1 = 1, 100, 4
do j1 = 1, 100, 16
do i2 = i1, i1 + 3
do j2 = j1, min(j1+15,100)
A(j2,i2) = A(j2,i2) + 1
end do; end do; end do; end do
end subroutine
subroutine func3(A)
implicit none
double precision :: A(100,100)
integer :: i1,i2,j1,j2, j
!! complete tiles
do i1 = 1, 100, 4
do j1 = 1, 96, 16
do i2 = i1, i1 + 3
do j2 = j1, j1 +15
A(j2,i2) = A(j2,i2) + 1
end do; end do; end do; end do
!! partial tiles / remainder
do i1 = 1, 100, 4
do i2 = i1, i1 +3
do j = 97, 100
A(j,i2) = A(j,i2) + 1
end do; end do; end do
end subroutine
subroutine func4(A)
implicit none
double precision :: A(100,100)
integer :: i1,i2,j1,j2, j
do i1 = 1, 100, 4
!! complete tiles
do j1 = 1, 96, 16
do i2 = i1, i1 + 3
do j2 = j1, j1 +15
A(j2,i2) = A(j2,i2) + 1
end do; end do; end do
!! partial tiles
do i2 = i1, i1 +3
do j = 97, 100
A(j,i2) = A(j,i2) + 1
end do; end do
end do
end subroutine
subroutine func5(A)
implicit none
double precision :: A(100,100)
integer :: i1,i2,j1,j2
do i1 = 1, 100, 4
do j1 = 1, 100, 16
do i2 = i1, i1 + 3
do j2 = j1, j1 +15
if (j2 < 101) A(j2,i2) = A(j2,i2) + 1
end do; end do; end do; end do
end subroutine
subroutine func6(A)
implicit none
double precision :: A(100,100)
integer :: i1,i2,j1,j2, i,j
!! complete tiles
do i1 = 1, 100, 4
do j1 = 1, 96, 16
do i2 = i1, i1 + 3
do j2 = j1, j1 +15
A(j2,i2) = A(j2,i2) + 1
end do; end do; end do; end do
!! partial tiles / remainder (not tiled)
do i = 1, 100
do j = 97, 100
A(j,i) = A(j,i) + 1
end do; end do
end subroutine
In the following example, function func7 tiles nested loops with a size of (4,16), resulting in partial tiles that cover the last 4 iterations of the j-loop, as in the previous example. However, the outer loop is parallelized with a parallel worksharing-loop construct.
Functions func8 and func9 illustrate two implementations of the tiling with parallel and worksharing-loop directives. Function func8 uses a single outer loop, with a min function to accommodate the partial tiles. Function func9 uses two sets of nested loops, the first iterates over the complete tiles and the second covers iterations from the partial tiles. When fissioning loops that are in a parallel worksharing-loop region, each iteration of each workshared loop must be executed on the same thread as in an un-fissioned loop. The schedule(static) clause in func7 forces the implementation to use static scheduling and allows the fission in function func8 . When dynamic scheduling is prescribed, fissioning is not allowed. When no scheduling is specified, the compiler implementation will select a scheduling kind and adhere to its restrictions.
//%compiler: clang
//%cflags: -fopenmp
/*
* name: partial_tile.2
* type: C
* version: omp_5.1
*/
int min(int a, int b){ return (a < b)? a : b; }
void func7(double A[100][100])
{
#pragma omp parallel for schedule(static)
#pragma omp tile sizes(4,16)
for (int i = 0; i < 100; ++i)
for (int j = 0; j < 100; ++j)
A[i][j] = A[i][j] + 1;
}
void func8(double A[100][100])
{
#pragma omp parallel for schedule(static)
for (int i1 = 0; i1 < 100; i1+=4)
for (int j1 = 0; j1 < 100; j1+=16)
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j2 = j1; j2 < min(j1+16,100); ++j2)
A[i2][j2] = A[i2][j2] + 1;
}
void func9(double A[100][100])
{
#pragma omp parallel
{
#pragma omp for schedule(static) nowait
for (int i1 = 0; i1 < 100; i1+=4)
for (int j1 = 0; j1 < 96; j1+=16)
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j2 = j1; j2 < j1+16; ++j2)
A[i2][j2] = A[i2][j2] + 1;
#pragma omp for schedule(static)
for (int i1 = 0; i1 < 100; i1+=4)
for (int i2 = i1; i2 < i1+4; ++i2)
for (int j = 96; j < 100; j+=1)
A[i2][j] = A[i2][j] + 1;
}
}
!!%compiler: gfortran
!!%cflags: -fopenmp
! name: partial_tile.2
! type: F-free
! version: omp_5.1
subroutine func7(A)
implicit none
double precision :: A(100,100)
integer :: i,j
!$omp parallel do schedule(static)
!$omp tile sizes(4,16)
do i=1,100
do j = 1, 100
A(j,i) = A(j,i) + 1
end do; end do
end subroutine
subroutine func8(A)
implicit none
double precision :: A(100,100)
integer :: i1,i2,j1,j2
do i1 = 1, 100, 4
do j1 = 1, 100, 16
do i2 = i1, i1 + 3
do j2 = j1, min(j1+15,100)
A(j2,i2) = A(j2,i2) + 1
end do; end do; end do; end do
end subroutine
subroutine func9(A)
implicit none
double precision :: A(100,100)
integer :: i1,i2,j1,j2,j
!$omp parallel
!$omp do schedule(static)
do i1 = 1, 100, 4
do j1 = 1, 96, 16
do i2 = i1, i1 + 3
do j2 = j1, j1 +15
A(j2,i2) = A(j2,i2) + 1
end do; end do; end do; end do
!$omp end do nowait
!$omp do schedule(static)
do i1 = 1, 100, 4
do i2 = i1, i1 +3
do j = 97, 100
A(j,i2) = A(j,i2) + 1
end do; end do; end do;
!$omp end parallel
end subroutine